Maclaurin Series: Derivation
This topic is usually taught after Differentiation Techniques, as the derivation of the Maclaurin Series formula can be explained by using differentiation.
To explain the derivation of the formula, we need to understand what is a power series first.
Maclaurin Expansion Derivation
Standard Expansions
With the understanding of the formula, let’s use it to find the series expansion of some common functions. These series can be found in the formula list MF26.
Maclaurin Series Standard Expansion Derivation
In this section, we will look at how series expansions of sums and products of various functions using standard series.
Maclaurin Series Standard Expansion Examples
Small Angles Approximation
The approximations of sin x and cos x for sufficiently small values of x can be made using the standard expansions. Here’s how.
Maclaurin Series Small Angles Approximation
Exam Questions with Full Solutions
5. Maclaurin Series Timed Practice Exam Questions’ SolutionsApplications of Maclaurin Series
The Maclaurin expansion is named after the Scottish mathematician, Colin Maclaurin. He was recognised for publishing a special case of the Taylor series in the 18th century. This formula is actually a member of Taylor series, where the values of a function’s derivatives are at any single point, besides zero.
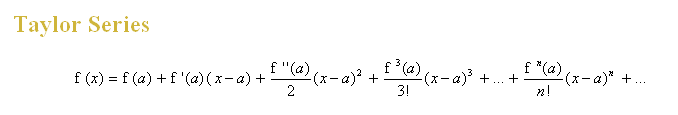
It has come across thousands of students why they are learning this topic. As the Maclaurin Series is just a special case of the Taylor Series, it would benefical to understand what real life applications there are for Taylor series.
As shown in the above Maclaurin examples, the Talyor series is a series in ascending powers of x which can be used to represent complicated functions as infinite polynomials. The series can used as a form of approximation for the complicated functions by using the first few non-zero terms. The more terms used, the less the answer deviates from the theoretical value.
Why shouldn’t we go for the exact value then? In a lot of real-life scenarios, it is not possible to have the precise answers. Approximations are sometimes good enough as they are more cost-efficient and less time consuming. It is a compromise between estimated values and complicated calculations. An example will be the integration of cos(x2). It will either be tedious to determine the integral or you can simply replace the expression with its Taylor series expansions. Integrating polynomials is definitely more fun!
The usage of Taylor series can be found in the fields of engineering, economics and modeling!